24. März 2024

Das „Traveling Salesman Problem“

Vor einigen Tagen wurde ich gefragt, ob ich wüsste, wie man die optimale Route für eine Strecke mit 250 Zwischenzielen planen kann. Also habe ich mich auf die Suche nach einer Lösung gemacht. Dass es für diese Aufgabenstellung Bachelor-Arbeiten und sogar einen schönen Fachbegriff gibt, wusste ich zu diesem Zeitpunkt noch nicht: Das „Traveling Salesman Problem“.

Das „Traveling Salesman Problem“ beschreibt das Problem bei dem ein Handlungsreisender den kürzesten Weg finden muss, um eine Reihe von Städten genau einmal zu besuchen und zum Ausgangspunkt zurückzukehren. Erstaunlicherweise bietet Google Maps hierfür keine Lösung. Hier kann man zwar Routen mit mehreren Reisezielen erstellen, die Möglichkeit die kürzeste Route mit allen Reisezielen zu errechnen, bietet Google aber nicht.

Also habe ich Chat GPT gebeten einige Koordinaten in die optimale Reihenfolge, mit der kürzesten Gesamtstrecke, zu bringen. Heraus kam ein Python-Skript, das die „Nearest Neighbor Heuristik“ verwendet, die zwar nicht unbedingt die optimalste Lösung liefert, aber für diesen Anwendungszweck oft ausreichend ist.

import math

# Funktion zur Berechnung der Entfernung zwischen zwei Koordinaten
def distance(coord1, coord2):
    lat1, lon1 = coord1
    lat2, lon2 = coord2
    # Radius der Erde in Kilometern
    radius = 6371.0  
    # Umrechnung von Grad in Radian
    lat1 = math.radians(lat1)
    lon1 = math.radians(lon1)
    lat2 = math.radians(lat2)
    lon2 = math.radians(lon2)
    # Deltas
    dlat = lat2 - lat1
    dlon = lon2 - lon1
    # Haversine-Formel zur Berechnung der Entfernung
    a = math.sin(dlat / 2)**2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2)**2
    c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
    distance = radius * c
    return distance

# Liste der Koordinaten
coordinates = [
    (50.938361, 6.959974),
    (53.550341, 10.000654),
    (48.1371079, 11.5753822),
    (52.5170365, 13.3888599),
    (52.3744779,9.7385532)
]

# Bestimme Startpunkt (erste Koordinate)
start_point = coordinates[0]
path = [start_point]
unvisited = set(coordinates[1:])

# Berechne den nächsten Punkt basierend auf der kürzesten Entfernung
while unvisited:
    nearest = min(unvisited, key=lambda x: distance(path[-1], x))
    path.append(nearest)
    unvisited.remove(nearest)

# Füge den Startpunkt am Ende hinzu, um den Rundweg zu schließen
path.append(start_point)

# Ausgabe der optimierten Reihenfolge der Koordinaten in einer GPX-Datei
with open("route.gpx", "w") as gpx_file:
    gpx_file.write('<?xml version="1.0" encoding="UTF-8" standalone="no" ?>\n')
    gpx_file.write('<gpx xmlns="http://www.topografix.com/GPX/1/1" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" version="1.1" creator="ChatGPT AI">\n')
    gpx_file.write(' <trk>\n')
    gpx_file.write('  <name>Route</name>\n')
    gpx_file.write('  <trkseg>\n')
    for point in path:
        gpx_file.write(f'   <trkpt lat="{point[0]}" lon="{point[1]}"/>\n')
    gpx_file.write('  </trkseg>\n')
    gpx_file.write(' </trk>\n')
    gpx_file.write('</gpx>\n')

print("Die Datei 'route.gpx' wurde erfolgreich erstellt.")

Aufklappen

Das Verfahren ist eigentlich sehr einfach und logisch: Beginnend bei Punkt A werden die Abstände zu allen anderen Punkten errechnet. Die nächste Koordinate ist die mit der kürzesten Entfernung. Von dort aus geht es weiter. Ausgehend von Koordinate B werden die Abstände zu allen anderen Punkten – außer Punkt A errechnet usw…

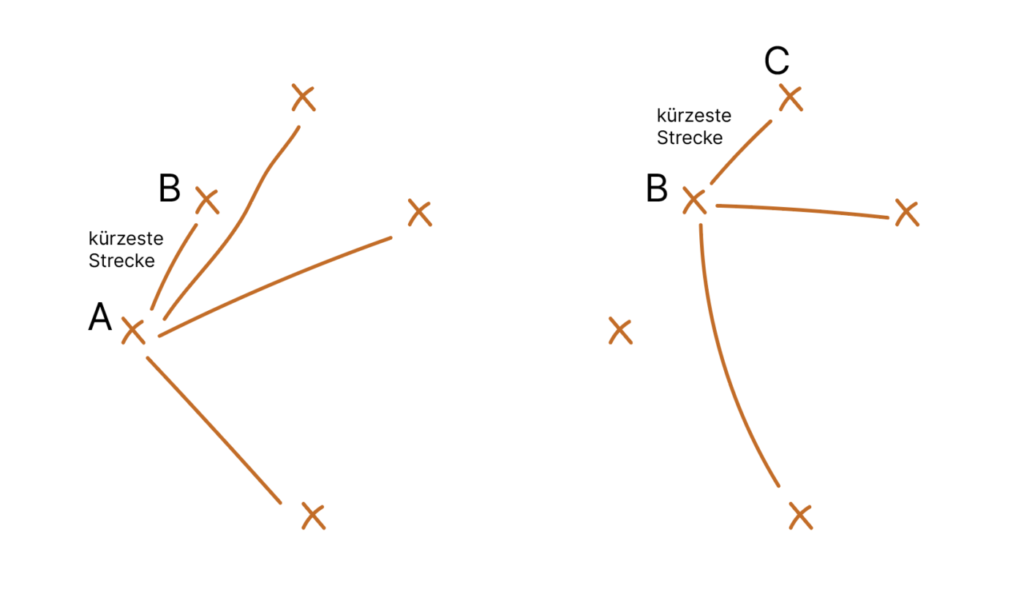
Was in der Theorie einfach ist, drückt sich im Code dann doch recht kompliziert aus. Ich bin zumindest sehr froh, dass ich den Code nicht selbst formulieren musste.

Ergebnis des oben gezeigten Codes ist eine gpx-Datei. Diese kann z.B. in Google MyMaps (https://www.google.com/maps/d/u/0/?hl=de) importiert werden. Allerdings werden hier nur die Punkte und Luftlinienverbindung dargestellt. Leider ist es nicht möglich hieraus eine Route zu generieren.

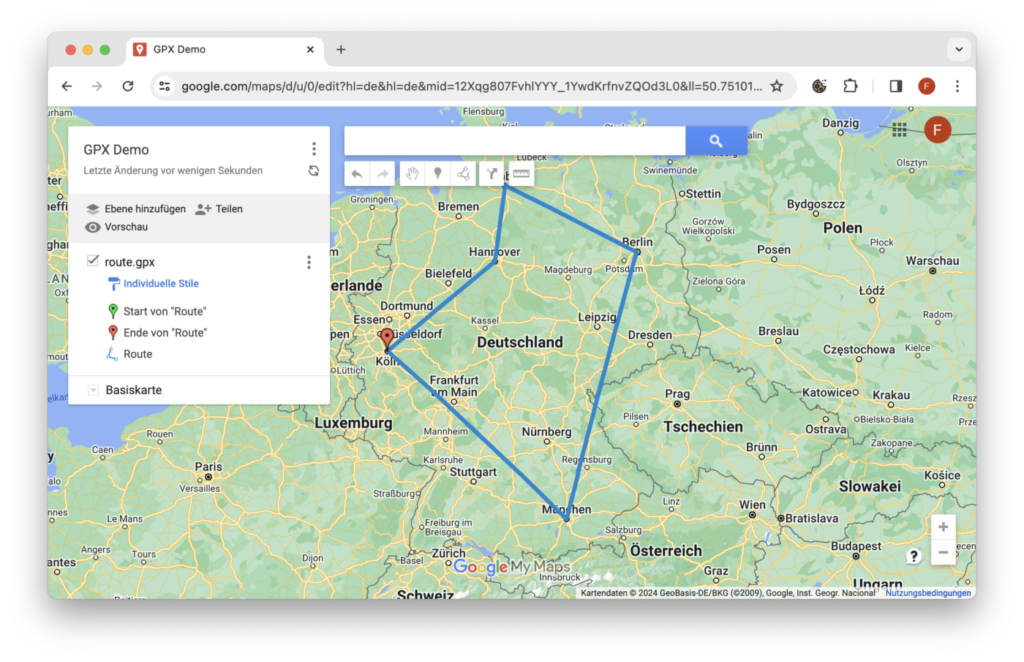
Eine konkrete Route kann hingegen auf brouter.de berechnet werden:

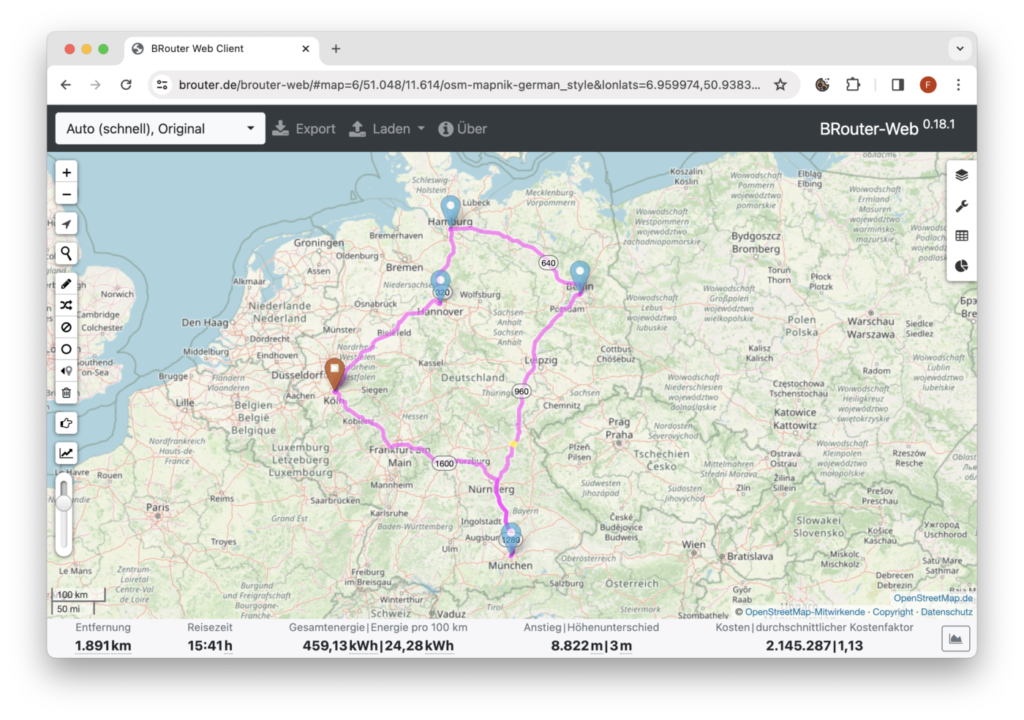
Um also konkret aus einer Liste mit Adressen eine optimale Route zu erstellen, sind folgende Schritte notwendig:

1. Alle Adressen auf Geoapify in Koordinaten umwandeln: www.geoapify.com/tools/geocoding-online
2. Die Koordinaten hier im GPX-Generator eintragen: www.fbnfrtg.de/tools/gpx-generator/
3. Die erzeugte gpx-Datei im Brouter Web-Client importieren https://brouter.de/brouter-web